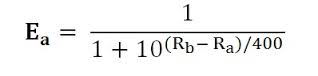For those few hearty souls who have attempted to read my disorganized rantings in the baseball shout box regarding my efforts to create a baseball player elo rating system based on match-up to match-up results, in sequence, allow me to summarize my experience to date, in a language so simple that it can be reduced to emojis:

IDEA PHASE:

:0

EXECUTION PHASE:

:D

DEBUG PHASE:

:|

RE-EXECUTION:

>(

SECOND DEBUG:

:) (!)

FINAL RUNS:

*DANCING*

NOTICE IDIOTIC TYPO:

:(

RERUN:

*headdesk*

Yep...the first serious attempt to turn the game of baseball into an elo-rated (and thus strength of schedule and clutch-corrected) system like chess was a total failure.  And the reason is so ridiculously obvious that someone on here should probably have stopped me from making a fool of myself except that I am terrible at explaining what I'm doing as I'm doing it and most of you have been reading my the first several words of my shouts on the topic and feeling as though I'm speaking in Swahili.  Sorry about that.  Let me now demonstrate how large of a moron I am in the simplest possible math terms (there are two formulas in this explanation, but that is unavoidable and I'll break them down.

HOW ELO WORKS

Before we can understand why Elo was never going to work on a match-up to match-up basis, and why my next idea has a much higher chance of success, we have to all get on the same page as to what it is that Elo is really doing. Elo affixes an easy to understand number onto a (hopefully) large sample of events as a means of expressing the probability of a win in the next game without having to think in terms of probabilities.  Here is the basic formula:

The answer to this one is never 42, so it's nothing too complex

Ra' refers to the altered Elo rating of any player, Ra is his rating before the game, K is an arbitrary weight that determines how much the rating can possibly change from game to game, Sa is the success rate of the player (1 for a W, 0.5 for a tie, and 0 for a loss), and Ea is the expected success rate given his initial rating and the rating of his opponent.  Seems simple enough, except that the final term must be found (all other terms are known except the new rating, after all), and it is found using a somewhat less simple formula:

Here's where I failed - let's see if you can spot it

Don't squint too hard at the equation, because it is simpler than it looks...it just takes this complex form because the creator needed a way to force the system to produce a ratings spread that is both easy to read and directly linked to the real odds of one player defeating another, which means he needed a final number between near-zero and near-one.  If the opponent has a higher rating than our original player, we surmise that the original man's odds of winning are less than 50%.  If the second player is a LOT better, we surmise that our guy is extremely unlikely to win.

Now look at the number in the numerator at the far right - that's called the spread term, and it determines how far apart the ratings should land between two players if one of them beats the other 91% of the time (if Rb - Ra = 400, then Ea becomes 1 / (10^1 + 1) or 1/11 (0.909).  The spread term is, essentially, arbitrary and an aesthetic choice for the person creating the ratings system, but the .909 W% is real and has meaning.  I just didn't see it quickly enough to reject my own bad idea.

BASEBALL MATCH-UPS:

Here's the problem, in baseball terms:

Batter A faces Pitcher B.  Both players are major leaguers and this is a big league game.  Do there exist any two players you could possibly imagine who could face each other and the odds of one of them producing or preventing more runs than expected in that situation are truly 91%?  Or...to put it more simply...is there any player match-up where you would expect the hitter to get on base at a .909 clip ---- or a .091 clip?  Other than some pitchers batting, perhaps?

Statistically, the answer to that question is no.  In fact, even if I were scoring Elo on a win/loss framework (run value of your event is positive, you get a W, negative you get an L), the range of Elo scores would be small because the true odds of victory, even for the pitcher, are something like 67% against an average hitter and 82% against a really bad one.  And, of course, that system would favor on base percentage and essentially ignore power (the magnitude of the run value of each event would not matter at all), and would cause just about every pitcher to have a high Elo score, and just about every hitter a low one.  The insight I somehow missed - Elo is self-correcting. It uses the data to tell a story about how often the various players have beaten each other, the lack of spread I was seeing in Elo ratings I produced was (a) entirely predictable (b) the surest sign that the system would never work to identify any skill, should it exist, for "playing up" against better competition and (c) made even worse by the fact that I was not trading in whole wins or whole losses, but, instead, on some percentage of a win determined by the run value of each event vs. the maximum run value possible in a given base/out state (a system where perhaps 95% of all plays have W% scores of between 0.35 and 0.80).

THE POSSIBLE SOLUTION:

When I realized this, I nearly gave up on Elo for baseball players entirely, thinking that there would be no way to correct for this reality that major league baseball players are tightly clustered in abilities, statistically.  But...I think I have a part of the answer now.

For Elo to work, I need a win/loss framework that doesn't penalize power hitters and favor players who get on base too much AND I need the probabilities of winning and losing between two players to reach 90+% and do so often enough that we can start to distinguish great players from good ones, and terrible players from bad ones.  I need to look at more than one match-up event at a time AND I need the clumps of events I look at to still be in a chronological sequence.   But how many events do I need to lump together to reach a point where the odds of, say, Felix Hernandez "beating" a league average hitter (producing a net negative run value) increase to 91%?

Felix Hernandez made the average hitter in the AL produce a wOBA of .241, which, for all intents and purposes, is the closest I can get on short notice to finding the linear-weighted odds that the average batter will beat Felix in any given match-up event.  What are the odds that the average hitter will have two conseucitve events against Felix that result in a net positive run value compared to average?  On three straight events? Four?  It turns out that your odds of net-beating Felix in 2014 in X consecutive events, if you were an average hitter, drop to about 10% after four plate appearances (I'll spare you the math showing this...it took me quite a while to think it through).  Which is, neatly, roughly one game.

THE CATCH:

Any attempt to lump events together and report on their net result will either blend match-ups in one time (and thus severely complicated the Elo rating of the "opponent" in any cluster), blend times in one match-up (and thus screw up the sequential nature of Elo), or do both.

Some ideas I've brainstormed for how I might go about gaining the larger frame of reference that I need to make Elo work:

1. I could let the sequence be the games played, rather than the order of events inside the games, and thus let the clusters be game/match-up groups...the three at bats Omar Vizquel got against Freddy Garcia in the game on May 23rd in 2001 could be one cluster, the one at bat Ichiro got off of Mariano Rivera in a different game could be another.  This poses two problems: it will work better for starting pitchers and starting position players, but even then, because of the preponderance of bullpen-usage and strategic pinch-hitting (and pitchers getting blown out early in starts and the like), it may bias toward OBP because there may be too many small clusters.
2. I could break a player's match-ups into sequential bins of size X (maybe 4 or 5?) in events and rate each bin, placing the Elo change for that match-up bin at the time of the final event.  This turns the sequential nature of Elo into more of a pseudo-sequence, and could be rather difficult to implement.
3. I could use the entire season's worth of match-up data and let the starting Elo rating be the rating from the end of the previous season...that would make seasonal Elo ratings impossible (or messy, at least), but would maximize bin sizes and improve Elo spread and the accuracy of each match-up report.
4. I could rate batters in binned events as in bullet #2, but with all-comers, rather than separated into individual match-ups (if the five events in a bin are against five different pitchers, I would need to find a "net Elo" of the opponents and there are a number of ways I could do that) - and the same could be done with pitchers.
5. I could use a rolling window approach.  For a particular batter, for example, I could look at the past X number of events, rate the net result, and make an Elo change, roll forward to the next event (adding one at the front and dropping one at the back of the window), re-evaluate the net result, and make a new rating change.  That would produce continuity...an Elo time series that has a new entry after each event...while also allowing for a larger frame of reference...but would be, easily, the most difficult method to implement.

THE SCARY THING:

I may be forced to try all of the above. Which...could take a while. But, I'm fopeful that my thinking on this problem will not be wasted.  I'll keep you all posted.